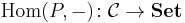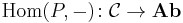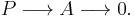Projective object

In category theory, the notion of a projective object generalizes the notion of a projective module.

An object P in a category C is projective if the hom functor

$\operatorname{Hom}(P,-)\colon\mathcal{C}\to\mathbf{Set}$

preserves epimorphisms. That is, every morphism f:P→X factors through every epi Y→X.

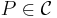Let $\mathcal{C}$ be an abelian category. In this context, an object $P\in\mathcal{C}$ is called a projective object if

$\operatorname{Hom}(P,-)\colon\mathcal{C}\to\mathbf{Ab}$

is an exact functor, where 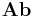$\mathbf{Ab}$ is the category of abelian groups.

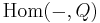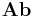The dual notion of a projective object is that of an injective object: An object $Q$ in an abelian category $\mathcal{C}$ is injective if the $\operatorname{Hom}(-,Q)$ functor from $\mathcal{C}$ to $\mathbf{Ab}$ is exact.

Enough projectives

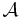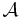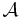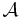Let $\mathcal{A}$ be an abelian category. $\mathcal{A}$ is said to have enough projectives if, for every object $A$ of $\mathcal{A}$ , there is a projective object $P$ of $\mathcal{A}$ and an exact sequence

$P \longrightarrow A \longrightarrow 0.$

In other words, the map 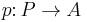$p\colon P \to A$ is "epi", or an epimorphism.

Examples.

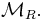
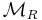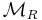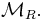Let $R$ be a ring with 1. Consider the category of left $R$ -modules $\mathcal{M}_R.$ $\mathcal{M}_R$ is an abelian category. The projective objects in $\mathcal{M}_R$ are precisely the projective left R-modules. So $R$ is itself a projective object in $\mathcal{M}_R.$ Dually, the injective objects in 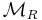$\mathcal{M}_R$ are exactly the injective left R-modules.

The category of left (right) $R$ -modules also has enough projectives. This is true since, for every left (right) $R$ -module $M$ , we can take $F$ to be the free (and hence projective) $R$ -module generated by a generating set $X$ for $M$ (we can in fact take $X$ to be $M$ ). Then the canonical projection $\pi\colon F\to M$ is the required surjection.

References

Mitchell, Barry (1965), Theory of categories, Pure and applied mathematics, 17, Academic Press, ISBN 978-0-124-99250-4, MR 0202787

This article incorporates material from Projective object on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License. This article incorporates material from Enough projectives on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.